OEIS/A291939: Difference between revisions
Jump to navigation
Jump to search
imported>Gfis Created page with "==First number on layer n of hailstone chain== The sequence had keyword <code>unkn</code> until March 2018, and there were only 5 terms: * 1, 12, 19, 27, 37 The comment read:..." |
imported>Gfis with .pl |
||
| Line 2: | Line 2: | ||
The sequence had keyword <code>unkn</code> until March 2018, and there were only 5 terms: | The sequence had keyword <code>unkn</code> until March 2018, and there were only 5 terms: | ||
* 1, 12, 19, 27, 37 | * 1, 12, 19, 27, 37 | ||
The comment | The original comment was: | ||
If hailstone chains are strictly drawn in numerical order at right angles with consistent | If hailstone chains are strictly drawn in numerical order at right angles with consistent | ||
direction, overlaps occur. The first set of numbers that do not overlap could be considered the | direction, overlaps occur. The first set of numbers that do not overlap could be considered the | ||
| Line 8: | Line 8: | ||
higher layer. This is the sequence of the first numbers to appear on layer n. | higher layer. This is the sequence of the first numbers to appear on layer n. | ||
''Hailstone chain'' is a synonym for Collatz sequences or the ''3n+1 problem'' - see [https://oeis.org/index/3#3x1 Index entries for sequences related to 3x+1 (or Collatz) problem]. | ''Hailstone chain'' is a synonym for Collatz sequences or the ''3n+1 problem'' - see [https://oeis.org/index/3#3x1 Index entries for sequences related to 3x+1 (or Collatz) problem]. | ||
==Generating Perl Program== | |||
[[File:A291939-3d.png|600px|right|First 5 terms of A291939]] | |||
After some experimenting it became clear that the description is incomplete, and that it is difficult to develop the sequence with 2-dimensional paper and pencil. The following Perl program generates the sequence, and it has a more detailled description at the beginning: | |||
<pre> | |||
<nowiki> | |||
#!perl | |||
# Build b-file of OEIS A291939 from Collatz sequences in A070165 | |||
== | # @(#) $Id$ | ||
# 2018-03-25, dr.georg.fischer@gmail.com | |||
#------------------------------------------------------ | |||
# Usage: | |||
# wget https://oeis.org/A070165/a070165.txt | |||
# perl a291939.pl 0 a070165.txt > b291939.txt | |||
# perl a291939.pl mode infile > outfile | |||
# mode = 0: print the raw b-file for A291939 | |||
# mode = 1: insert additional comments for the 3D structure | |||
# mode = 2: show additional trace data | |||
# Sequence: | |||
# 1, 12, 19, 27, 37, 43, 51, 55, 75, 79, ... 9997 | |||
# Explanation: | |||
# Take the Collatz sequences (CSs) from A070165, and build a 3-dimensional | |||
# structure representing all CSs up to some starting number (10000). | |||
# In that 3D structure, the y direction is downwards, x is to the right, | |||
# and the "layer" z is outside. | |||
# Process all CSs with increasing starting number coln = 1, 2, 3 ... 10000. | |||
# Begin at the end of any CS (4 2 1), and proceeding up to | |||
# the starting number. Name the elements e(1) = 1, e(2) = 2, e(3) = 4 etc. | |||
# Position the trailing element e(1) = 1 at coordinates (x,y,z) = (0,0,0). | |||
# Investigate all e[i] (i > 1): | |||
# for even e[i] "go right" = store e[i] at (e[i-1)].(x+1), e[i-1].y, e[i-1].z), | |||
# for odd e[i] "go down" = store e[i] at (e[i-1)].x, e[i-1].(y+1), e[i-1].z), | |||
# whenever that position is not occupied by a different number, | |||
# otherwise "go up", i.e. increase the layer z by one for all new elements | |||
# to be stored from now on. | |||
# The target sequence A291939 = a(n) consists of the starting | |||
# values of the CSs which reach a z coordinate of n for the first | |||
# time. | |||
#-------------------------------------------------------- | |||
use strict; | |||
my $mode = 1; # 0 = b-file only, 1 = with 3D coordinates, 2 = more trace output | |||
if (scalar(@ARGV) > 0) { | |||
$mode = shift(@ARGV); | |||
} | |||
my $bfn = 1; # index for target b-file | |||
my $layer = 1; | |||
my @elems; # maps elements of a CS to their coordinates (x,y,z) | |||
$elems[1] = "0,0,0"; | |||
my %coords; # maps (x,y,layer=z) -> elements of a CS | |||
$coords{$elems[1]} = 1; | |||
print <<"GFis"; | |||
# b-file for A291939, n=1..1769, generated by perl $0 $mode a070165.txt | |||
1 1 | |||
GFis | |||
my @colseq = (); | |||
my $curr_layer = 0; | |||
while (<>) { | |||
next if ! m{\A\d}; # no digit in column 1 -> skip initial comment lines | |||
# 9/20: [9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
s/\s+//g; # remove all spaces | |||
my ($pair,$cs) = split(/\:/); | |||
my ($coln, $count) = split(/\//, $pair); # CS starts at $coln and has $count elements | |||
$cs =~ s{[\[\]]}{}; # remove square brackets | |||
@colseq = split(/\,/, $cs); | |||
if ($mode >= 2) { | |||
print "# evaluate CS($coln) = " . join(" ", @colseq) . "\n"; | |||
} | |||
my ($x, $y, $z) = split(/\,/, $elems[1]); | |||
my $ind = scalar(@colseq) - 1; | |||
$ind --; # element's indexes run backwards in contradiction to the explanation above | |||
while ($ind >= 0) { | |||
my $elcurr = $colseq[$ind]; | |||
if (defined($elems[$elcurr])) { | |||
($x, $y, $z) = split(/\,/, $elems[$elcurr]); | |||
} else { # undefined - append to chain | |||
if (($elcurr & 1) == 0) { # even -> go right | |||
$x ++; | |||
&investigate($coln, $elcurr, $x, $y, $curr_layer); | |||
} else { # odd -> go down | |||
$y ++; | |||
&investigate($coln, $elcurr, $x, $y, $curr_layer); | |||
} | |||
} # undefined | |||
$ind --; | |||
} # while $ind | |||
} # while <> | |||
#-------- | |||
sub investigate { | |||
my ($coln, $elcurr, $x, $y, $z) = @_; | |||
if (defined($coords{"$x,$y,$z"})) { | |||
my $stelem = $coords{"$x,$y,$z"}; | |||
if ($stelem ne $elcurr) { # collision | |||
$curr_layer ++; | |||
$z = $curr_layer; | |||
if ($mode >= 1) { | |||
print "# collision ,$x,$y,$z,$elcurr,$coln // $stelem, layer=$curr_layer\n"; | |||
} | |||
$bfn ++; | |||
print "$bfn $coln\n"; # print the b-file entry | |||
&allocate($elcurr, $x, $y,$z); | |||
} # else same element - ignore | |||
} else { # undefined | |||
&allocate($elcurr, $x, $y,$z); | |||
} # undefined | |||
} # investigate | |||
#-------- | |||
sub allocate { | |||
my ($elcurr, $x, $y, $z) = @_; | |||
$coords{"$x,$y,$z"} = $elcurr; | |||
$elems[$elcurr] = "$x,$y,$z"; | |||
if ($mode >= 1) { | |||
print "# coords ,$x,$y,$z,$elcurr\n"; | |||
} | |||
} # allocate | |||
</nowiki></pre> | |||
==Input Collatz sequences== | |||
The program reads the first 10000 Collatz sequences from [https://oeis.org/A070165/a070165.txt a070165.txt]: | |||
<pre> | |||
<nowiki> | |||
content of https://oeis.org/A070165/a070165.txt follows: | |||
This file has 10000 rows showing the following for each row: | |||
a) Starting number for Collatz sequence ending with 1 (a.k.a. 3x+1 sequence). | |||
b) Number of terms in sequence (a.k.a. number of halving and tripling steps to reach 1). | |||
c) Actual sequence as a vector. | |||
1/4: [1, 4, 2, 1] | |||
2/2: [2, 1] | |||
3/8: [3, 10, 5, 16, 8, 4, 2, 1] | |||
4/3: [4, 2, 1] | |||
5/6: [5, 16, 8, 4, 2, 1] | |||
6/9: [6, 3, 10, 5, 16, 8, 4, 2, 1] | |||
7/17: [7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
8/4: [8, 4, 2, 1] | |||
9/20: [9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
10/7: [10, 5, 16, 8, 4, 2, 1] | |||
11/15: [11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
12/10: [12, 6, 3, 10, 5, 16, 8, 4, 2, 1] | |||
13/10: [13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
14/18: [14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
15/18: [15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
16/5: [16, 8, 4, 2, 1] | |||
17/13: [17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
18/21: [18, 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
19/21: [19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
20/8: [20, 10, 5, 16, 8, 4, 2, 1] | |||
21/8: [21, 64, 32, 16, 8, 4, 2, 1] | |||
22/16: [22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
23/16: [23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
24/11: [24, 12, 6, 3, 10, 5, 16, 8, 4, 2, 1] | |||
25/24: [25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
26/11: [26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
27/112: [27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
28/19: [28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
29/19: [29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
30/19: [30, 15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
31/107: [31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
32/6: [32, 16, 8, 4, 2, 1] | |||
33/27: [33, 100, 50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
34/14: [34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
35/14: [35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
36/22: [36, 18, 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
37/22: [37, 112, 56, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
... | |||
10000/30: [10000, 5000, 2500, 1250, 625, 1876, 938, 469, 1408, 704, 352, 176, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] | |||
</nowiki> | |||
</pre> | |||
Revision as of 18:38, 25 March 2018
First number on layer n of hailstone chain
The sequence had keyword unkn until March 2018, and there were only 5 terms:
- 1, 12, 19, 27, 37
The original comment was:
If hailstone chains are strictly drawn in numerical order at right angles with consistent direction, overlaps occur. The first set of numbers that do not overlap could be considered the 'first layer'. Once an overlap is needed, all numbers farther up the chain (inclusive) are on a higher layer. This is the sequence of the first numbers to appear on layer n.
Hailstone chain is a synonym for Collatz sequences or the 3n+1 problem - see Index entries for sequences related to 3x+1 (or Collatz) problem.
Generating Perl Program
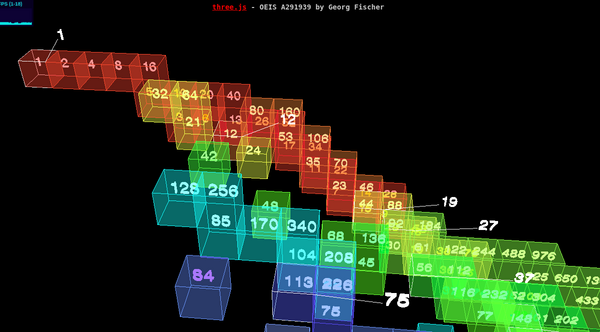
After some experimenting it became clear that the description is incomplete, and that it is difficult to develop the sequence with 2-dimensional paper and pencil. The following Perl program generates the sequence, and it has a more detailled description at the beginning:
#!perl
# Build b-file of OEIS A291939 from Collatz sequences in A070165
# @(#) $Id$
# 2018-03-25, dr.georg.fischer@gmail.com
#------------------------------------------------------
# Usage:
# wget https://oeis.org/A070165/a070165.txt
# perl a291939.pl 0 a070165.txt > b291939.txt
# perl a291939.pl mode infile > outfile
# mode = 0: print the raw b-file for A291939
# mode = 1: insert additional comments for the 3D structure
# mode = 2: show additional trace data
# Sequence:
# 1, 12, 19, 27, 37, 43, 51, 55, 75, 79, ... 9997
# Explanation:
# Take the Collatz sequences (CSs) from A070165, and build a 3-dimensional
# structure representing all CSs up to some starting number (10000).
# In that 3D structure, the y direction is downwards, x is to the right,
# and the "layer" z is outside.
# Process all CSs with increasing starting number coln = 1, 2, 3 ... 10000.
# Begin at the end of any CS (4 2 1), and proceeding up to
# the starting number. Name the elements e(1) = 1, e(2) = 2, e(3) = 4 etc.
# Position the trailing element e(1) = 1 at coordinates (x,y,z) = (0,0,0).
# Investigate all e[i] (i > 1):
# for even e[i] "go right" = store e[i] at (e[i-1)].(x+1), e[i-1].y, e[i-1].z),
# for odd e[i] "go down" = store e[i] at (e[i-1)].x, e[i-1].(y+1), e[i-1].z),
# whenever that position is not occupied by a different number,
# otherwise "go up", i.e. increase the layer z by one for all new elements
# to be stored from now on.
# The target sequence A291939 = a(n) consists of the starting
# values of the CSs which reach a z coordinate of n for the first
# time.
#--------------------------------------------------------
use strict;
my $mode = 1; # 0 = b-file only, 1 = with 3D coordinates, 2 = more trace output
if (scalar(@ARGV) > 0) {
$mode = shift(@ARGV);
}
my $bfn = 1; # index for target b-file
my $layer = 1;
my @elems; # maps elements of a CS to their coordinates (x,y,z)
$elems[1] = "0,0,0";
my %coords; # maps (x,y,layer=z) -> elements of a CS
$coords{$elems[1]} = 1;
print <<"GFis";
# b-file for A291939, n=1..1769, generated by perl $0 $mode a070165.txt
1 1
GFis
my @colseq = ();
my $curr_layer = 0;
while (<>) {
next if ! m{\A\d}; # no digit in column 1 -> skip initial comment lines
# 9/20: [9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1]
s/\s+//g; # remove all spaces
my ($pair,$cs) = split(/\:/);
my ($coln, $count) = split(/\//, $pair); # CS starts at $coln and has $count elements
$cs =~ s{[\[\]]}{}; # remove square brackets
@colseq = split(/\,/, $cs);
if ($mode >= 2) {
print "# evaluate CS($coln) = " . join(" ", @colseq) . "\n";
}
my ($x, $y, $z) = split(/\,/, $elems[1]);
my $ind = scalar(@colseq) - 1;
$ind --; # element's indexes run backwards in contradiction to the explanation above
while ($ind >= 0) {
my $elcurr = $colseq[$ind];
if (defined($elems[$elcurr])) {
($x, $y, $z) = split(/\,/, $elems[$elcurr]);
} else { # undefined - append to chain
if (($elcurr & 1) == 0) { # even -> go right
$x ++;
&investigate($coln, $elcurr, $x, $y, $curr_layer);
} else { # odd -> go down
$y ++;
&investigate($coln, $elcurr, $x, $y, $curr_layer);
}
} # undefined
$ind --;
} # while $ind
} # while <>
#--------
sub investigate {
my ($coln, $elcurr, $x, $y, $z) = @_;
if (defined($coords{"$x,$y,$z"})) {
my $stelem = $coords{"$x,$y,$z"};
if ($stelem ne $elcurr) { # collision
$curr_layer ++;
$z = $curr_layer;
if ($mode >= 1) {
print "# collision ,$x,$y,$z,$elcurr,$coln // $stelem, layer=$curr_layer\n";
}
$bfn ++;
print "$bfn $coln\n"; # print the b-file entry
&allocate($elcurr, $x, $y,$z);
} # else same element - ignore
} else { # undefined
&allocate($elcurr, $x, $y,$z);
} # undefined
} # investigate
#--------
sub allocate {
my ($elcurr, $x, $y, $z) = @_;
$coords{"$x,$y,$z"} = $elcurr;
$elems[$elcurr] = "$x,$y,$z";
if ($mode >= 1) {
print "# coords ,$x,$y,$z,$elcurr\n";
}
} # allocate
Input Collatz sequences
The program reads the first 10000 Collatz sequences from a070165.txt:
content of https://oeis.org/A070165/a070165.txt follows: This file has 10000 rows showing the following for each row: a) Starting number for Collatz sequence ending with 1 (a.k.a. 3x+1 sequence). b) Number of terms in sequence (a.k.a. number of halving and tripling steps to reach 1). c) Actual sequence as a vector. 1/4: [1, 4, 2, 1] 2/2: [2, 1] 3/8: [3, 10, 5, 16, 8, 4, 2, 1] 4/3: [4, 2, 1] 5/6: [5, 16, 8, 4, 2, 1] 6/9: [6, 3, 10, 5, 16, 8, 4, 2, 1] 7/17: [7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 8/4: [8, 4, 2, 1] 9/20: [9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 10/7: [10, 5, 16, 8, 4, 2, 1] 11/15: [11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 12/10: [12, 6, 3, 10, 5, 16, 8, 4, 2, 1] 13/10: [13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 14/18: [14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 15/18: [15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] 16/5: [16, 8, 4, 2, 1] 17/13: [17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 18/21: [18, 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 19/21: [19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 20/8: [20, 10, 5, 16, 8, 4, 2, 1] 21/8: [21, 64, 32, 16, 8, 4, 2, 1] 22/16: [22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 23/16: [23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] 24/11: [24, 12, 6, 3, 10, 5, 16, 8, 4, 2, 1] 25/24: [25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 26/11: [26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 27/112: [27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] 28/19: [28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 29/19: [29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 30/19: [30, 15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] 31/107: [31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] 32/6: [32, 16, 8, 4, 2, 1] 33/27: [33, 100, 50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 34/14: [34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 35/14: [35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1] 36/22: [36, 18, 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] 37/22: [37, 112, 56, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1] ... 10000/30: [10000, 5000, 2500, 1250, 625, 1876, 938, 469, 1408, 704, 352, 176, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1]